Cloth Estimation

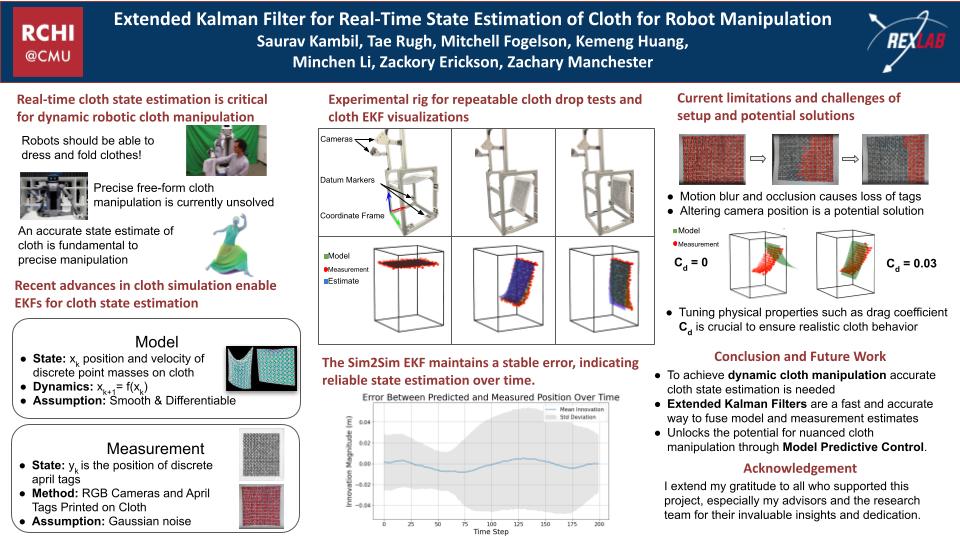
In the Robotic Exploration Lab at Carnegie Mellon, I worked on a project to do state estimation of cloth. Robotic manipulation of nonrigid objects is a dificult task that people care about, i.e. “why can’t a robot fold my clothes?”. A large part of this problem is with estimating the state of the object and predicting how it will interact with its surroundings. We wanted to see what results we could achieve with a model-based approach.

Simulation

We used a Codimensional Incremental Potential Contact (C-IPC) model for the cloth, courtesy of Professor Minchen Li. The state of the cloth is defined as the 3 dimensional position and velocity of each node of the mesh. Node density is important for the accuracy of the simulation, but also quickly increases the size of the state vector.

Estimation

I built an Extended Kalman Filter in C++ to estimate the state of cloth using this simulation.

For our demonstrations, we used a rectangular mesh with uniformly distributed nodes. As such, if we had nodes along $m$ rows and $n$ columns, we would have $6 * m * n$ state variables. We performed drop tests where one edge of the cloth was held fixed while the rest were released.

We first tested with artificial measurements, where I took a subset of nodes and added noise to their position to use as a “measurement”. I also dropped some of these node measurements from frame to frame to simulate missing measurements.

Measurement

For the real-world test, we arranged 2 cameras from top and front perspectives of the cloth. The cloth had printed April Tags arranged in a grid to easily give us a subset of node measurements.

Results

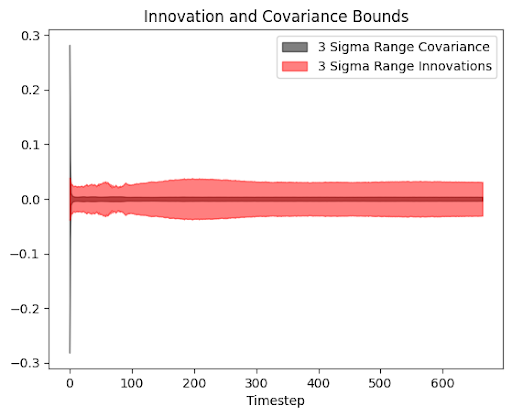
With camera blur, we had a significant amount of measurement dropout for the lower April Tags during the fastest part of the cloth drop. We also left simulation parameters such as elasticity to reasonable but untuned values. Likely due to the high amount of measurement dropout at the beginning of the cloth drop, the estimate was a bit unstable in the first few frames. But after this, the Kalman Filter managed to overcome these imperfections in both measurement and model, and converged to a relatively stable estimation.

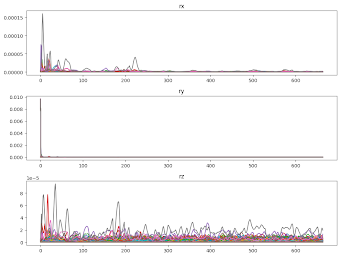
The covariance of all states quickly dropped to near-zero and the innovations remained bounded.